Yr Hafaliad Ton

Hafaliad d'Alembert

Mae hafaliad d'Alembert yn rhoi datrysiad yr hafaliad ton homogenaidd \(u_{xx}-c^2u_{tt}=0\) yn ddibynnol ar yr amodau cychwynnol sy'n diffinio'r proffil dadleoliad (hynny yw \(u(x,0)=f(x)\)) a'r proffil cyflymder cychwynnol \(\text{(h.y. }u_t(x,0)=g(x)\text{).}\) Yna rhoir y datrysiad fel

\[\begin{split} \begin{aligned} u(x,t) &= \frac{1}{2}\!\left(f(x+ct)+f(x-ct)\right) \\ &\qquad + \frac{1}{2c}\int_{x-ct}^{x+ct} g(\lambda)\,d\lambda. \end{aligned} \end{split}\]

Adnabyddir problem o'r math yma gydag amodau cychwynnol fel problem Cauchy.

Deillio hafaliad d'Alembert

Derivation of d'Alembert's equation

Datrysiad ar linyn hyd-meidraidd

Mae'r hafaliad ton ar linyn hyd-meidraidd gydag amodau cychwynnol a ffin addas (e.e., terfynau sefydlog) yn enghraifft o broblem Sturm-Liouville. Gellir ei ddatrys trwy ddarganfod datrysiad gwahanadwy ar ffurf

\[ u(x,t)=X(x)T(t). \]

Trwy amnewid y ffurf yma mewn i'r hafaliad differol rhannol ac ad-drefnu, gallwn ostwng y broblem i ddau hafaliad differol cyffredin trefn dau, un ar gyfer \(X(x)\) a'r llall ar gyfer \(T(t)\). Ymddangosir hyn oherwydd bod un ochr yr hafaliad differol cyffredin yn ffwythiant o \(t\) yn unig, a'r llall yn ffwythiant o \(x\) yn unig; gan fod y rhain yn newidynnau annibynnol, mae'n rhaid bod y ddau ochr yn hafal i gysonyn. Wrth ddatrys y broblem ar gyfer \(X(x)\) byddwn yn darganfod, fel arfer, y bodola datrysiadau annistadl ar gyfer gwerthoedd penodol o'r gysonyn blaenorol yn unig. Galwn y fath werthoedd yn werthoedd eigen.

Mae'r egwyddor arsodiad yn ein galluogi i ysgrifennu'r datrysiad ar ffurf cyfres anfeidraidd. Yna gallwn ddefnyddio cyfres Fourier er mwyn pennu cyfernodau yn y datrysiad cyffredinol sy'n galluogi'r amodau cychwynnol i gael eu bodloni.

Gweler eich nodiadau darlithoedd ar gyfer y manylion.

Hafaliad Duhamel - hafaliad ton anhomogenaidd

Rhoir hafaliad ton anhomogenaidd un-dimensiynol fel

\[ u_{tt}-c^2u_{xx}=h(x,t). \]

Mae cynnwys y ffwythiant \(h(x,t)\) yn modelu tardd y tonnau.

Gwelon yn y darlithoedd y rhoir datrysiad yr hafaliad ton anomogenaidd gyda'r amodau cychwynnol homogenaidd

\[ u(x,0)=0, \]

\[ u_t(x,0)=0, \]

fel

\[ u(x,t)=\frac{1}{2c}\int\limits_{0}^t\int\limits_{x-c(t-\tau)}^{x+c(t-\tau)}h(y,\tau)\mathrm{d}y\mathrm{d}\tau. \]

Deillio hafaliad Duhamel

Derivation of Duhamel's equation

Animeiddiadau o ddatrysiadau i'r hafaliad ton homogenaidd

Mae'r animeiddiadau isod yn enghreifftio datrysiadau i'r broblem Cauchy ar gyfer yr hafaliad ton homogenaidd 1-D

\[ u_{tt}-c^2u_{xx}=0, \]

with initial conditions \(u(x,0)=f(x)\) ac \(u_t(x,0)=g(x)\). Fel rydym wedi gweld yn y darlithoedd, rhoddir datrysiadau i'r broblem hyn gan fformiwla d'Alembert:

\[\begin{split} \begin{aligned} u(x,t) &= \frac{1}{2}\!\left(f(x+ct)+f(x-ct)\right) \\ &\qquad + \frac{1}{2c}\int_{x-ct}^{x+ct} g(\lambda)\,d\lambda. \end{aligned} \end{split}\]

Ym mhob achos sydd wedi'i blotio isod, mae \(c=1\).

Plotiau syml o ddatrysiad d'Alembert

Os hoffech roi cynnig arni i wneud rhai eich hunain, cliciwch ar gyfer y cod Python.

Y ffwythiant Gaussaidd (\(e^{-x^2}\)) dadleoliad cychwynnol, cyflymder cychwynnol yn sero

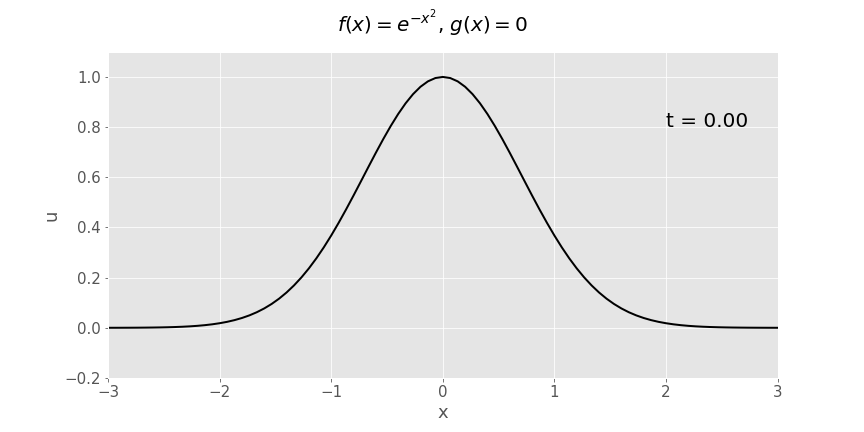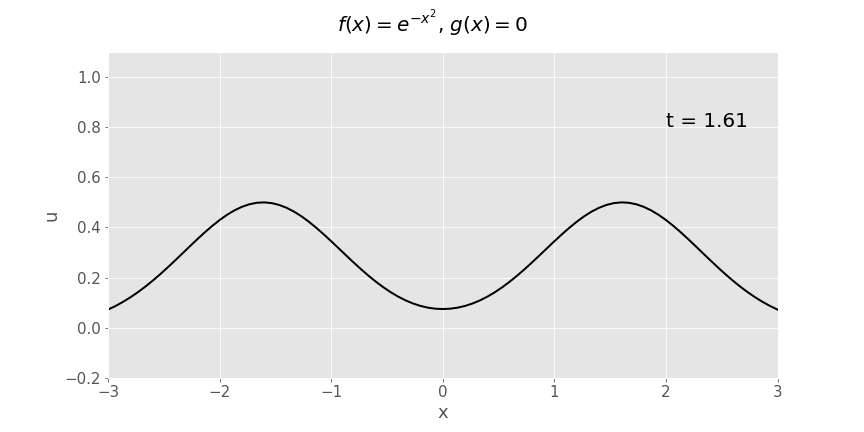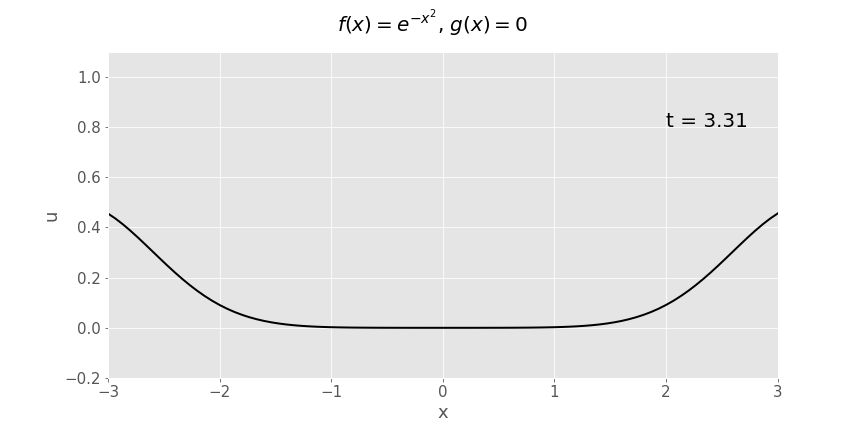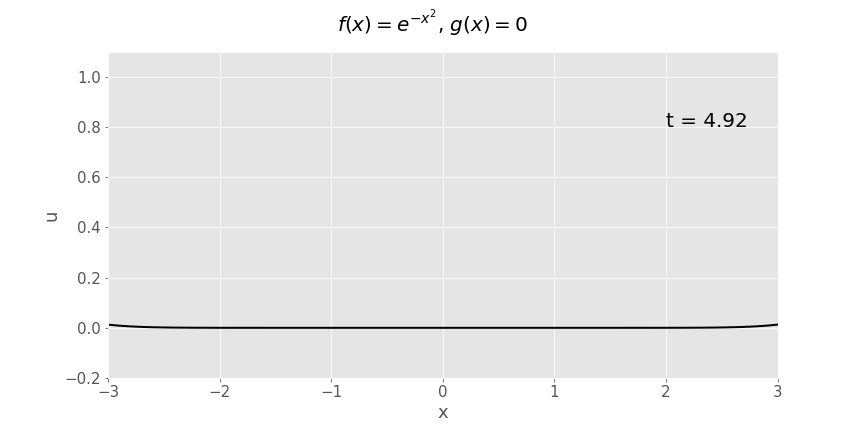
Ffordd arall i blotio yr union un ffwythiant o \(x\) a \(t\) yw plot arwyneb:

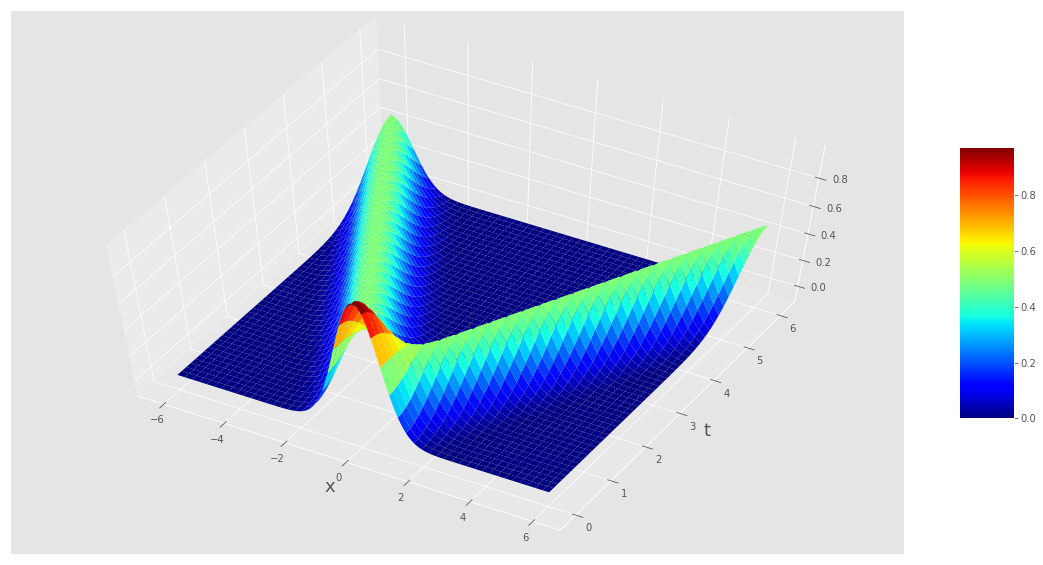
Nodwch y tebygrwydd rhwng y plot hyn a'r brasluniau rydym wedi lluniadu yn y darlithoedd pan yn trafod syniadau sy'n berthynol i achosiaeth.

Y ffwythiant Gaussaidd (\(e^{-x^2}\)) dadleoliad cychwynnol, cyflymder cychwynnol sinwsoidaidd (\(\frac{1}{10}\sin x\))

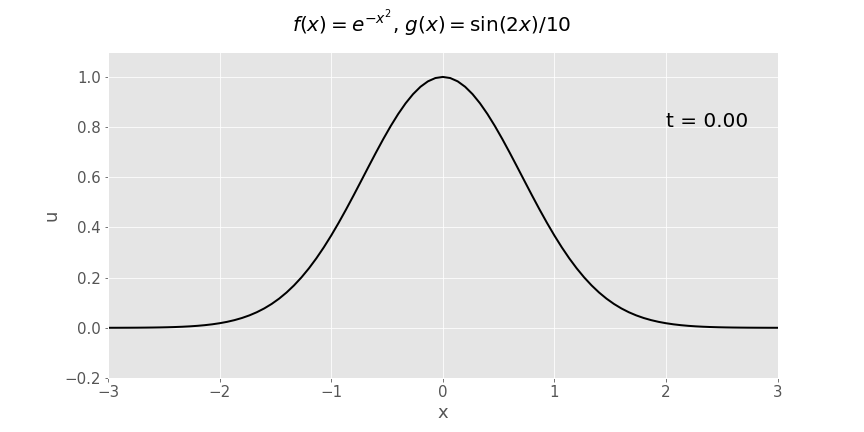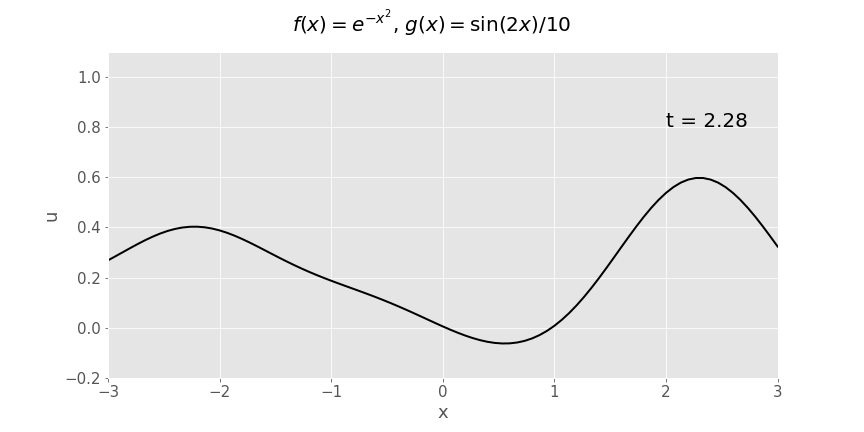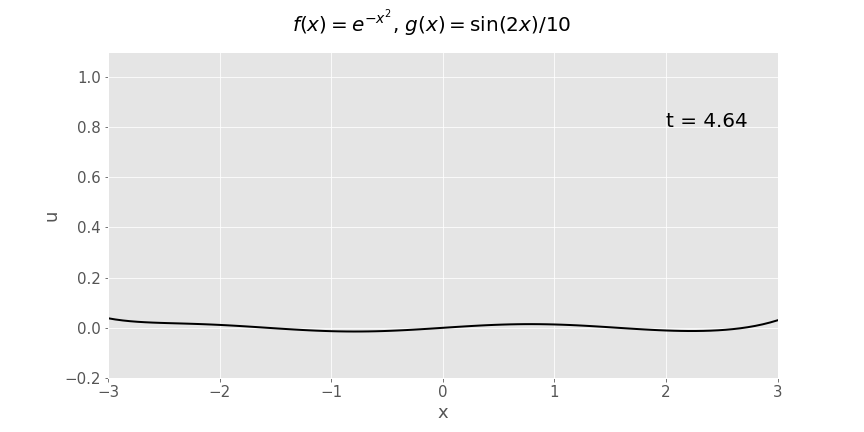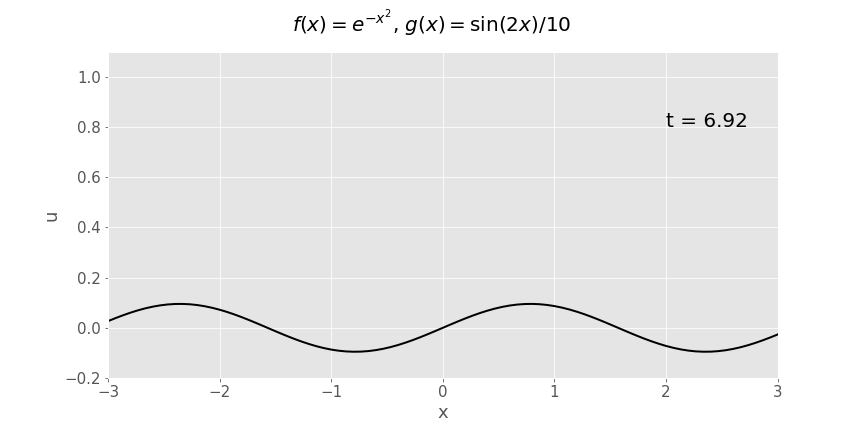
Adlewyrchiad

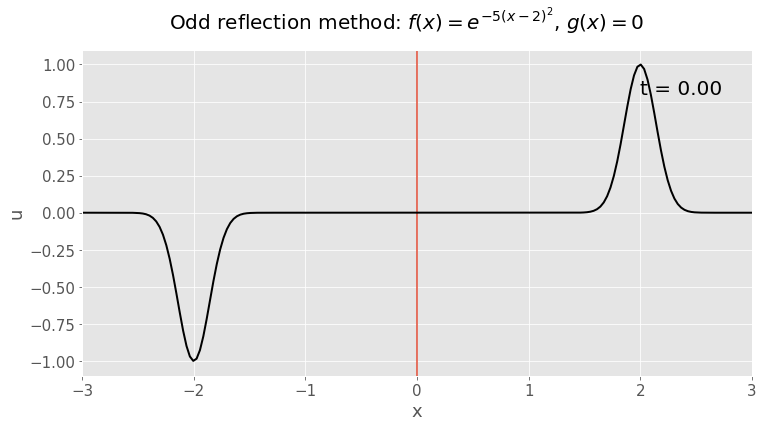
Tybiwch ein bod eisiau datrys yr hafaliad ton ar linyn hanner-anfeidraidd ar \(x>0\), gyda dadleoliad cychwynnol \(u(x,0)=f(x)=e^{-5(x-2)^2}\) a chyflymder cychwynnol \(u_t(x,0)=g(x)=0\). Ar ddiwedd y llinyn (\(x=0\)), rydym yn gosod y dadleoliad yn sero, felly \(u(0,t)=0\) ar gyfer pob \(t>0\).

Rydym wedi gweld yn y darlithoedd bod y ffordd i ddelio gyda'r broblem yma yw od-adlewyrchiad, lle rydym yn estynu'r amodau cychwynnol trwy eu hadlewyrchu mewn modd od fel eu bod wedi'u diffinio ar gyfer pob \(x\in\mathbb{R}\).

Dangosir hyn yn yr animeiddiad isod. Llun o'r amod cychwynnol yw'r ffram gyntaf, felly gallwch weld yr od-adlewyrchiad yn glir.

Dyma'r animeddiad os gadawn i amser i redeg:

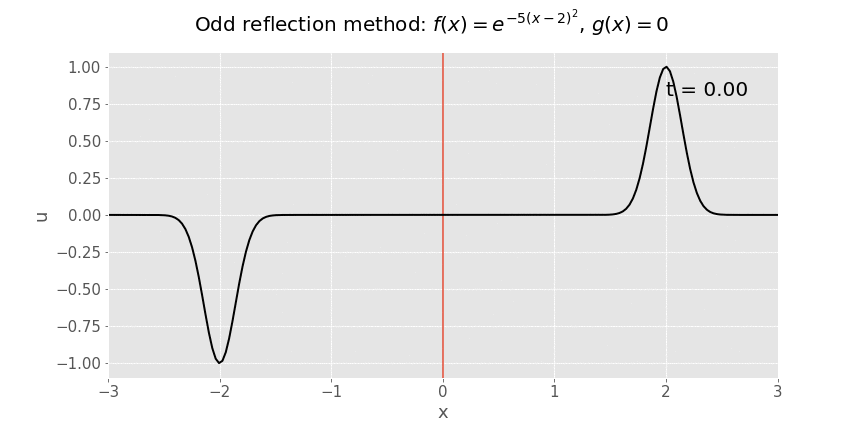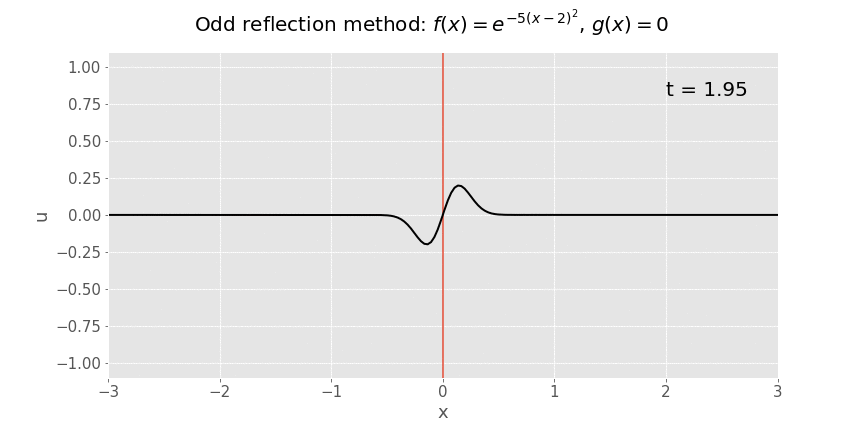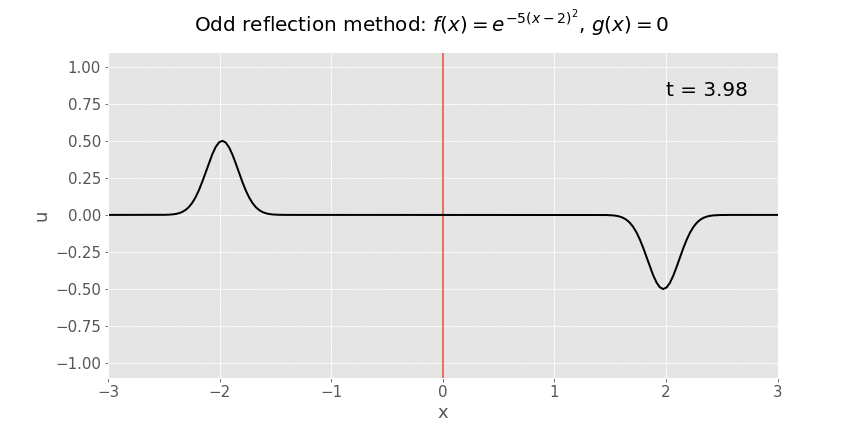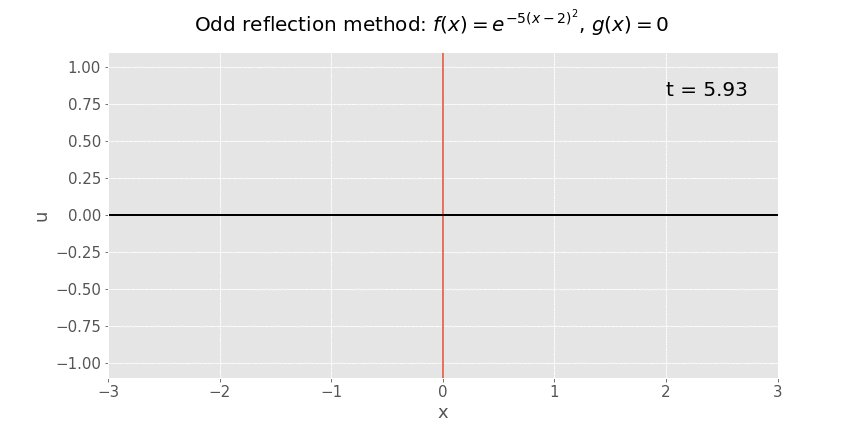
Y datrysiad i'r broblem gwreiddiol yw cyfyngiad y datrysiad i \(x\) bositif, h.y. popeth i'r dde o'r llinell coch. Mae popeth i'r chwith o'r llinell coch yn declun fathemategol yn unig, sy'n ein galluogi i ddefnyddio fformiwla d'Alembert. Mae natur od yr adlewyrchiad yn sicrhau bod yr amod ffin ar ddiweddbwynt y llinyn yn cael ei fodloni.